
गोपनीयता कथन: तपाईंको गोपनीयता हाम्रो लागि धेरै महत्त्वपूर्ण छ। हाम्रो कम्पनीले तपाईंको व्यक्तिगत जानकारीलाई तपाईंको स्पष्ट अनुमतिहरू बाहिर निकाल्ने अनुमति दिदैन।
+86-0510-86199063
1 Introduction
After the 1980s, power electronics technology developed rapidly. The use of various frequency converters, converters, switching power supplies and reactors is increasing. The resulting harmonic pollution is also becoming more and more serious, causing severe distortion of the voltage and current of the power system. Affect the normal operation of instrumentation, increase the loss of power devices, and endanger the safe operation of the power system. At present, harmonic pollution has become one of the serious public hazards of the power system. It is especially urgent to solve the harmonic problem of power system. Power system harmonics are very broad, including harmonic detection, harmonic analysis, harmonic source analysis, power grid harmonics calculation, harmonic suppression, and harmonic standards. Harmonic detection is an important branch of harmonic problems and the basis for solving other harmonic problems. The harmonics of the power system are affected by randomness, distribution, non-stationary factors, etc. It is not easy to accurately detect them. With the wide application of power electronic devices, harmonic and reactive power problems have become a research hotspot. In 1983, Japanese scholar Akagi Thai proposed the theory of instantaneous reactive power of three-phase circuits, also known as pq theory, which proposed a new method for harmonic and reactive power detection of three-phase circuits.
2 Three-phase instantaneous reactive power theory based on ip-iq
In order to overcome the insufficiency of the voltage quality caused by the pq theory detection, the pq theory has been continuously developed and improved to form a three-phase instantaneous reactive power theory based on ip-iq. The core idea of the theory is to obtain the ip, iq by passing the three-phase current satisfying ia+ib+ic=0 through the Park transformation without the zero sequence component. which is:
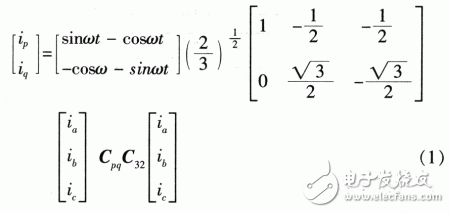
It can be seen that the current detection is only related to the electrical angle ωt of the A-phase voltage, and the distortion of the voltage wave has no effect on the detection result. Where C32 is a three-phase to two-phase coordinate transformation matrix; Cpq is a rotational coordinate transformation matrix. When the three-phase current is symmetrical, the detected current is:

Where k is an integer, ω is the angular frequency, and Ikm and θk are the magnitude and initial phase of each current. Substituting (2) into (1) gives the following formula:

When k=l, 7, 13... take the symbol; when k=5, 11, 17... remove the symbol.
As can be seen from equation (4), ![]() Corresponding to the active current and reactive current of the fundamental component in the conventional sense. Because ip and iq can be separated by LPF to obtain DC component
Corresponding to the active current and reactive current of the fundamental component in the conventional sense. Because ip and iq can be separated by LPF to obtain DC component ![]() If will
If will ![]() At the same time, the inverse transform can obtain the fundamental component iaf, ibf, icf as follows:
At the same time, the inverse transform can obtain the fundamental component iaf, ibf, icf as follows:

Where C23 is a two-phase to three-phase coordinate transformation array. In turn, the harmonic currents iah, ibh, and ich are:

Further analysis of the harmonic currents iah, ibh, ich can obtain the specific conditions of the higher harmonics contained in the three-phase alternating current, so that real-time detection of high-order harmonics and targeted filtering control can be realized.
If iq is only inversely transformed by (1), the instantaneous value iaq, ibq, icq of the reactive current component is obtained as follows:

The instantaneous reactive current in the three-phase alternating current can be separated by the equation (7) without delay. In practice, the control system can be designed according to the current value to realize fast reactive power compensation. It can be seen that the theory of instantaneous reactive power of three-phase circuits provides a theoretical basis for the rapid detection of reactive currents and higher harmonic currents.
3 Harmonic and reactive current detection based on reactive power theory
After the three-phase instantaneous reactive power theory is proposed, it is quickly used for the detection of harmonics and reactive currents in power systems due to its real-time performance in detecting current. And with the further development of this theory, various detection methods are derived. Representative ones are: p-q detection method and ip-iq detection method. The following describes the detection method of p-q:
The method calculates p-g according to the definition, when the voltage wave is not distorted (that is, a standard sine wave), and the current contains reactive and harmonic components:

Where k is an integer representing the harmonic order and ω is the angular frequency; Ikm and ψk are the amplitude and initial phase of each current.
Transform (8) into the αβ coordinate system and substitute it into (5):

Where n = 3k+1. When n=3k+1, the formula (9) is taken as a symbol; when n=3k-1, the equation (9) is taken out. It can be seen that the formula (9) can be divided into two parts, wherein the first half is a DC component corresponding to n=1, that is, the fundamental wave active and the fundamental wave reactive in power. The latter part is the power of the AC part corresponding to n"l, that is, the higher harmonics in power are active and reactive. The calculation block diagram when detecting harmonics by this detection method is shown in Fig. 1.

The detection method is briefly described as follows. First, the three-phase voltage and current values ua, ub, uc, and ia, ib, and ic obtained by sampling are subjected to αβ transformation to obtain uα, uβ, and iα, iβ; and p, q is calculated by definition; The DC component p, q in p, q is obtained by a low-pass filter; and p, q are inversely transformed with each other to obtain fundamental wave current components iaf, ibf, and icf in the three-phase current. The three-phase currents ia, ib, ic are subtracted from the fundamental current components iaf, ibf, icf to obtain the higher harmonic components iah, ibh, ich in the current. When the grid voltage is undistorted, the fundamental wave can be seen from the above derivation. The detection of the current components iaf, ibf, icf is accurate, so that the detected values of the higher harmonic components iah, ibh, ich are also accurate. The following is a discussion of the detection when the grid voltage is distorted.
Set the grid voltage to:


It can be seen from the above equation that the DC component p, q contains not only the fundamental active power (reactive power) but also the active power (reactive power) generated by the higher harmonics, so that the three-phase current calculated by the equation The fundamental current components iaf, ibf, and icf must have errors, so that the detected higher harmonic components iaha, ibht, and ich also have errors. This is also the biggest shortcoming of the pq detection algorithm. To detect the sum current of the harmonic current and the reactive current for comprehensive compensation, the detection block diagram of Figure 2 can be used.

In the detection and detection block diagram, only low-pass filtering processing is performed on p, and q is not filtered. Inverting p and q to obtain the fundamental current components iaf, ibf, and icf in the three-phase current. At this time, iaf, ibf, and icf only contain the fundamental active current component; subtracting the three-phase currents ia, ib, and ic The fundamental current components, iaf, ibf, and icf, obtain the sum currents iah+q, ibh+q, and ich+q of the higher harmonics and reactive currents in the current.
4 Conclusion
Accurate and real-time detection of harmonic currents and reactive currents in the power grid is the key to suppressing harmonics and reactive power compensation. According to the instantaneous reactive power theory, the three-phase harmonic current is detected. The feasibility and effectiveness of the harmonic detection method based on instantaneous reactive power theory are proved, and accurate and real-time harmonic and reactive components are provided for suppressing harmonic and reactive power compensation.
October 23, 2023
August 16, 2023
January 16, 2024
यस आपूर्तिकर्तामा ईमेल गर्नुहोस्
October 23, 2023
August 16, 2023
January 16, 2024

गोपनीयता कथन: तपाईंको गोपनीयता हाम्रो लागि धेरै महत्त्वपूर्ण छ। हाम्रो कम्पनीले तपाईंको व्यक्तिगत जानकारीलाई तपाईंको स्पष्ट अनुमतिहरू बाहिर निकाल्ने अनुमति दिदैन।

अधिक जानकारी भर्नुहोस् ताकि तपाईं छिटो सम्पर्कमा जान सक्नुहुन्छ
गोपनीयता कथन: तपाईंको गोपनीयता हाम्रो लागि धेरै महत्त्वपूर्ण छ। हाम्रो कम्पनीले तपाईंको व्यक्तिगत जानकारीलाई तपाईंको स्पष्ट अनुमतिहरू बाहिर निकाल्ने अनुमति दिदैन।